Sesgos y cómo detectarlos II
Camila Larrosa
26/09/2022
Siguiendo con la serie de artículos respecto la temática de Ética y Algoritmos, y concretamente sobre Fairlearn, en esta publicación dejaremos la teoría de lado y aplicaremos un ejemplo práctico de mitigación de inequidad utilizando la herramienta Fairlearn. Este análisis esta a disposicion en el sitio web de Fairlearn, allí puedes verlo con más detalle, así como tener acesso a los guías de usuario de la heramienta, los códigos utilizados y otros ejemplos.
En este estudio de caso comprobaremos la existencia o no de sesgos cometidos por un modelo de clasificación, para la toma de decisiones de préstamos. Puedes consultar más profundamente el conjunto de datos utilizados en el sitio, aunque te adelanto que el dataframe disponibilizado por sklearn contiene informaciónes personales como: nivel educativo, ocupación, sueldo, género, país de domicilio, entre otras.
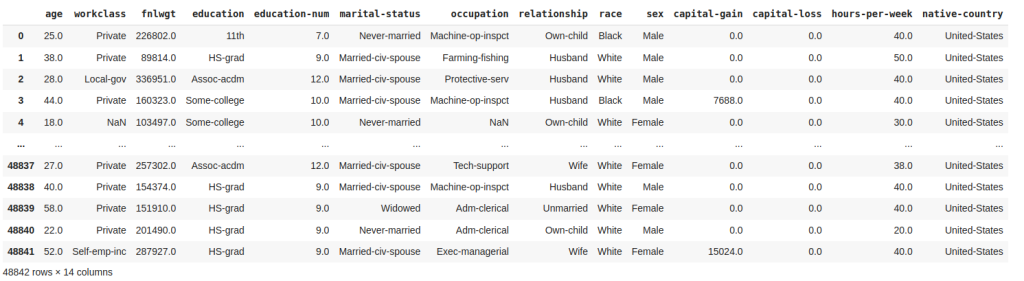
Consideraremos que el modelo se está produciendo para un Banco muy preocupado con la cuestión de género. Por eso, este cliente quiere saber si su conjunto de datos contiene algún sesgo de este tipo y, siendo así, ya tiene planes para lanzar un programa en el que pondrá más préstamos a disposición de las mujeres para fomentar el espíritu empresarial femenino.
Por tanto, el género de la persona que solicita el préstamo será nuestra variable sensible.
A = df[[‘sex’]]
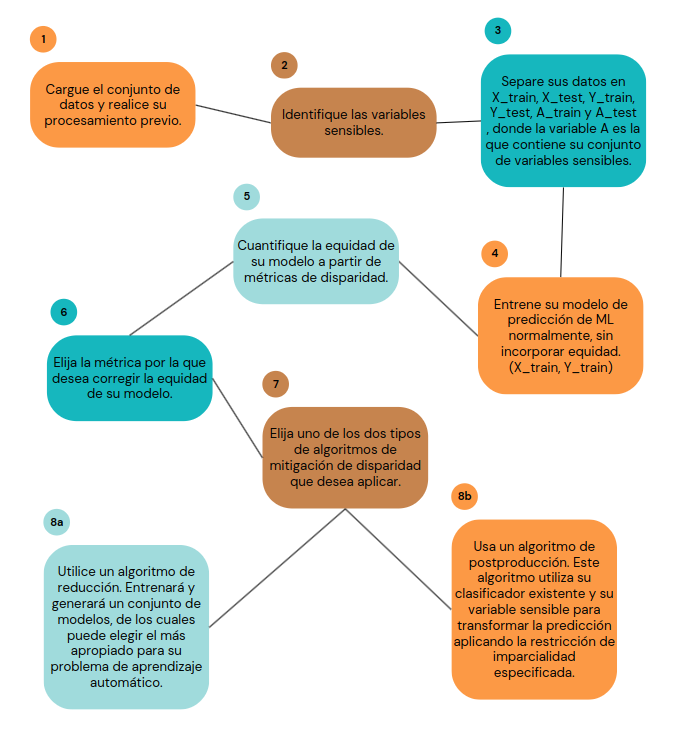
Tras entender el problema y haber seleccionado una (o varias) variables sensibles, trabajamos con los datos de forma análoga al comportamiento habitual: manipulación, entrenamiento, pruebas y selección de un modelo apropiado de aprendizaje automático.
Una vez hecho esto, ahora comenzaremos a usar las bibliotecas de Fairness. Primero, identificamos y cuantificamos si existe disparidad demográfica para la variable sensible del género (sex) de la persona que solicita el préstamo.
Para eso utilizamos la función MetricFrame, donde debemos definir qué métrica queremos medir (en este caso, tasa de selección, precisión y contagenen de seleccionados de cada género), así como cuál es la variable sensible utilizada para el test del modelo (A_test), la variable objetivo de test (Y_test) y la variable de salida (Y_pred).
MetricFrame(metrics={«accuracy»: skm.accuracy_score,
«selection_rate»: selection_rate,
«count»: count},
sensitive_features = A_test[‘sex’],
y_true = Y_test,
y_pred = unmitigated_predictor.predict(X_test));
A través de los resultados obtenidos por la función MetricFrame, generamos tablas y gráficos para analizar la paridad demográfica del modelo.
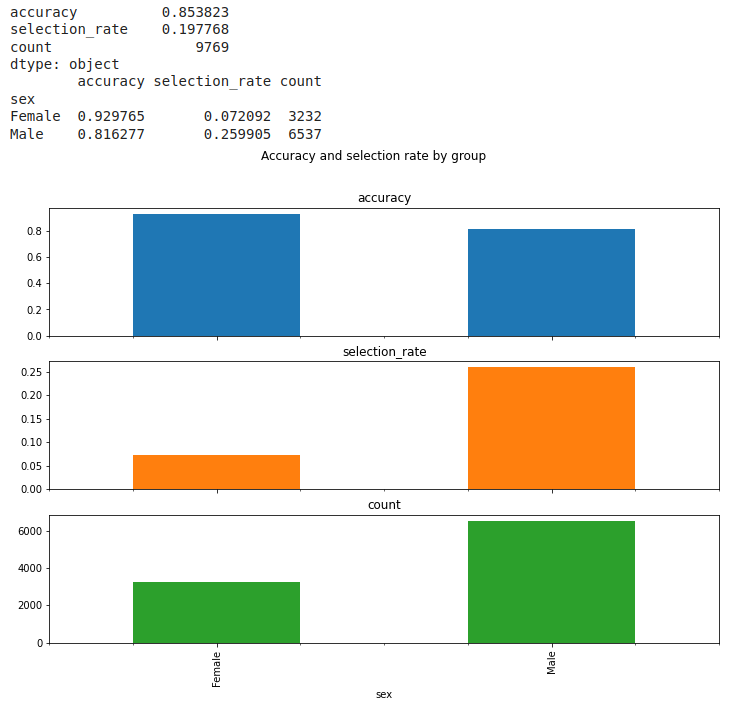
Mirando los resultados podemos sacar las siguientes conclusiones:
1) Con respecto a la precisión: El algoritmo puede hacer una predicción un poco mejor para el grupo de las mujeres. Es decir, aproximadamente el 93% de la variabilidad de la clase mujeres es explicada por el modelo, mientras que para la clase hombres, se explica 82% de la variabilidad;
2) La tasa de selección para el grupo de hombres es casi 4 veces mayor que para el grupo de mujeres. O sea, se ha comprobado una disparidad de oportunidades, pues los hombres reciben préstamos a una tasa mayor que las mujeres;
3) En cuanto al cómputo total de hombres y mujeres seleccionados para recibir el préstamo: 3232 mujeres fueron seleccionadas, ya en relación a los hombres, el número fue más que el doble, en el orden de 6537.
También podemos probar si las probabilidades son iguales para la variable sensible. Para ello, utilizaremos la misma función MetricFrame y los mismos parámetros utilizados para la paridad demográfica, con la excepción, por supuesto, de la variable métrica.
En este caso:
metrics={«false positive rate»: false_positive_rate,
«false negative rate»: false_negative_rate}
A través de los resultados obtenidos por la función MetricFrame en relación a probabilidades igualadas, generamos tablas y gráficos para su análisis.
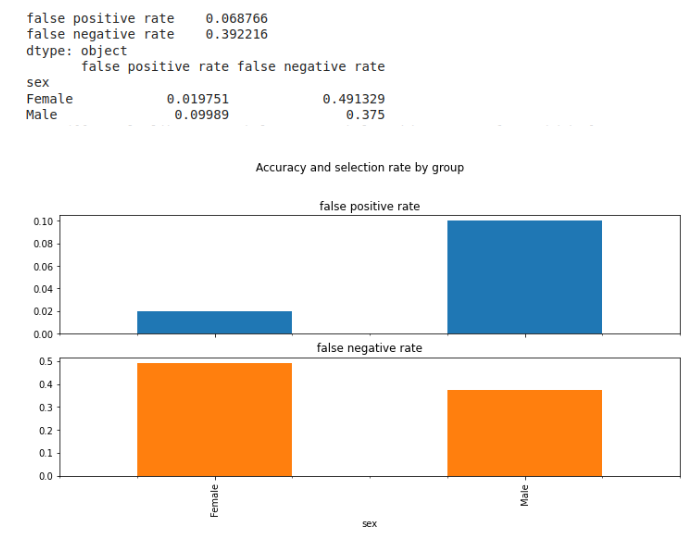
Podemos observar a través de las tasas de falsos positivos y falsos negativos que:
1) La tasa de falsos positivos para hombres es más de 5 veces mayor que para mujeres. Es decir, hay más hombres que están clasificadas como que podrían recibir un préstamo, cuando en la realidad, no están aptos;
2) Al mismo tiempo, la tasa de falsos negativos para mujeres se presenta también más grande que para los hombres. Eso es, hay un error de clasificación mayor para las mujeres, las cuales se clasifican como como no aptas a recibir el préstamo en un número mayor, cuando en realidad si son aptas a nivel de condiciones;
3) Por lo tanto, también se probó la existencia de probabilidades desiguales entre hombres y mujeres reproducidas por el modelo.
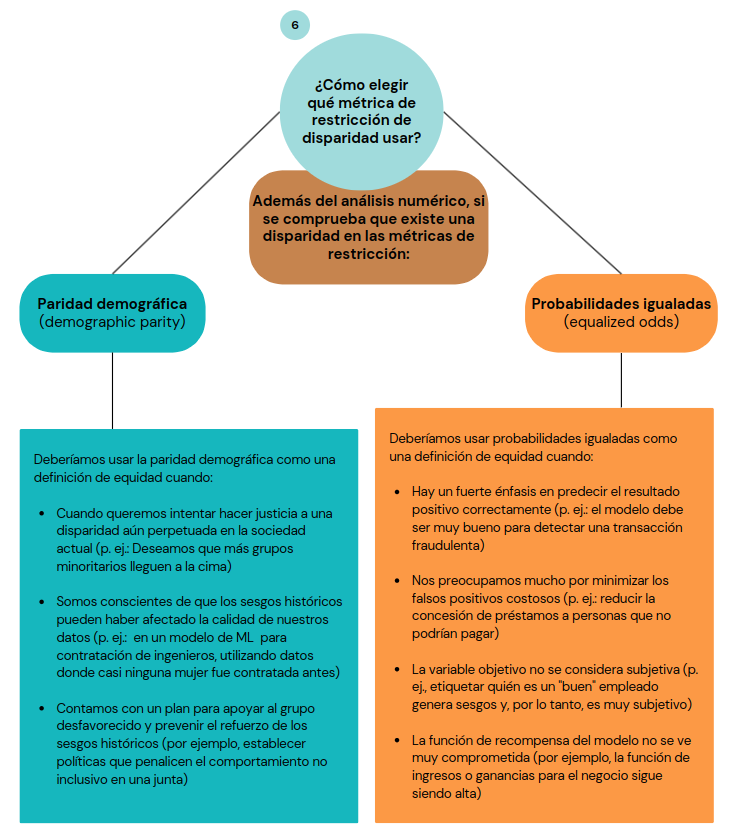
Y ahora, ¿cual de las dos métricas elegir como referencia de equidad para el clasificador? En este caso, lo ideal sería utilizar la paridad demográfica, te explico porqué.
Somos conscientes de que, históricamente, las mujeres ganan salarios más bajos que los hombres, por lo que los datos probablemente tengan este sesgo. Determinada la métrica, otra elección que debe hacerse en este punto es: ¿Qué algoritmo de mitigación de inequidad de Fairlearn usar? ¿Por reducción o posprocesamiento? Veamos cómo se solucionaría en ambos casos.
Primero hagámoslo por el método del algoritmo de reducción, usando fairlearn.reductions.GridSearch. Esta clase implementa una versión simplificada de la reducción de gradiente exponenciada de Agarwal.
Debes proporcionar a la función un estimador de aprendizaje automático predeterminado, la métrica elegida para la corrección y el tamaño de la muestra. GridSearch irá generar una secuencia de cambios de nombre y pesos, y entrenará un predictor para cada uno.
GridSearch(LogisticRegression(),
constraints = DemographicParity(),
grid_size = 71)
El siguiente paso sería trazar las métricas de rendimiento y de equidad de estos predictores. Eso se puede hacer a través del Dashboard que ofrece Fairlearn (FairnessDashboard) o a través de un gráfico con todos los modelos generados en la etapa anterior.
Finalmente, podemos evaluar los modelos dominantes junto con el modelo no mitigado.
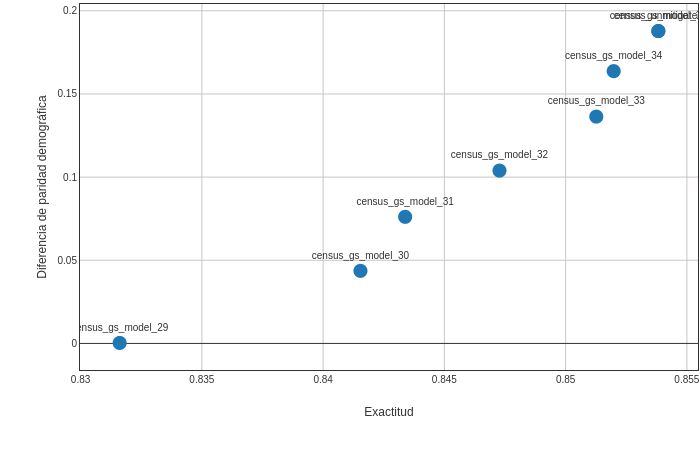
Vemos la formación de un frente de Pareto: el conjunto de predictores que representan las compensaciones óptimas entre la exactitud y la disparidad en las predicciones.
En el caso ideal, tendríamos un predictor en el punto (1,0), perfectamente exacto y sin ninguna injusticia bajo la paridad demográfica (con respecto a la característica sensible: género).
El frente de Pareto representa lo más cerca que podemos llegar a este ideal según nuestros datos y la elección del estimador. Y atención a los ejes del gráfico: el eje de disparidad cubre más valores que la exactitud, por lo que podemos reducir la disparidad sustancialmente para una pequeña pérdida de exactitud.
¿Qué modelo elegir para poner en producción? En un ejemplo real, elegimos el modelo que represente la mejor compensación entre exactitud y disparidad dadas las restricciones comerciales relevantes.
Veamos el mismo resultado desde la perspectiva de un algoritmo de posprocesamiento: para eso, Fairlearn ofrece el algoritmo ThresholdOptimizer, que sigue el enfoque de Hardt, Price y Srebro.
ThresholdOptimizer toma un modelo de aprendizaje automático existente cuyas predicciones actúan como una función de puntuación e identifica un umbral separado para cada grupo con el fin de optimizar alguna métrica objetiva específica (como la precisión) sujeta a restricciones de equidad específicas (como paridad demográfica).
Por lo tanto, el clasificador resultante es solo una versión con un umbral adecuado del modelo de aprendizaje automático subyacente.
Para llamar la función ThresholdOptimizer necesitamos las siguientes variables: El modelo existente que deseamos umbralizar, la métrica de rendimiento del modelo (que acaba por restringir la disparidad, por eso el nombre) y la métrica objetiva que queremos maximizar (métrica de disparidad).
postprocess_est = ThresholdOptimizer(
estimator = LogisticRegression(),
constraints = ‘demographic_parity’,
objective = ‘accuracy_score’,
grid_size=71)
Además, para usar ThresholdOptimizer, necesitamos especificar las características sensibles durante el entrenamiento y una vez implementado:
postprocess_est.fit(X_train, Y_train, sensitive_features=A_train.sex)
Y_pred_postprocess = postprocess_est.predict(X_test, sensitive_features=A_test.sex)
Teniendo todas las métricas de interés para la evaluación de los modelos posprocesado (mitigado) y el modelo no mitigado, podemos comparar los dos clasificadores:
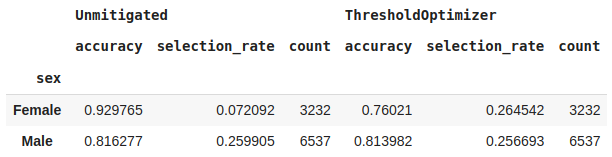
Al usar el algoritmo de mitigación de posprocesamiento, la precisión del modelo mitigado para mujeres disminuyó un poco, sin embargo, la tasa de selección de préstamos entre hombres y mujeres se volvió la misma, es decir, ahora hay la misma oportunidad entre los 2 géneros.
En conclusión, el mensaje principal de esta serie de artículos es que los datos, que provienen de nuestra historia, pueden estar llenos de sesgos injustos que nuestros modelos perpetúan de forma sistemática y automatizada. Como empresa, o persona que manipula datos, o incluso como ciudadanos, debemos reflexionar y encontrar soluciones viables a este gravísimo problema.
Estamos al comienzo de este vasto camino, que incluye no solo cuestiones técnicas, sino también sociales. Desde Datarmony estamos trabajando para poder detectar mejor estos sesgos y producir algoritmos más justos. Nuestro objetivo pasa por compartir con vosotros este conocimiento y ayudar a que el mundo del aprendizaje automático pueda aportarnos cada día más.
Referencias bibliográficas:
Hardt, M., Price, E., & Srebro, N. (2016). Equality of opportunity in supervised learning. Advances in neural information processing systems, 29.
Witt, D. M., Nieuwlaat, R., Clark, N. P., Ansell, J., Holbrook, A., Skov, J., … & Guyatt, G. (2018). American Society of Hematology 2018 guidelines for management of venous thromboembolism: optimal management of anticoagulation therapy. Blood advances, 2(22), 3257-3291.