Métodos de clasificación – Machine Learning
Aplicados a la predicción de cancelación de reservas
Felipe Maggi
10/01/2023
La cancelación de reservas es un problema que afecta en general a todas las empresas del sector de viajes y turismo. Hoteles y aerolíneas lidian con él como parte de su día a día, y desde que se ha generalizado el uso de plataformas online, el cambio de comportamiento de los usuarios lo ha potenciado. En Internet, la competencia está a un click de distancia, y nos hemos acostumbrado a tener disponibles muchas ofertas de lo mismo. Es fácil encontrar un precio mejor.
Las cancelaciones, en cualquier caso, no solo se producen porque se encuentra una oferta similar a menor coste. También hay cambios de planes, imprevistos familiares o laborales y pandemias que obligan a suspender viajes, por citar solo algunas causas.
Incluso aplicándose costes de cancelación, cosa que las líneas aéreas suelen hacer, el esfuerzo de cancelar una reserva online por parte del usuario es mínimo, en muchos casos. De hecho, una de las formas de potenciar la finalización de la venta es ofrecer opciones de cancelación ventajosas y sencillas. El mensaje que recibe el usuario es más o menos el siguiente: “reserva ahora, no pasa nada grave si luego te arrepientes”. Es una pescadilla que se muerde la cola.
La situación es compleja. Las reservas canceladas implican costes de gestión y pérdida de ingresos si la plaza no se alcanza a revender. Atacar el problema a través de la sobreventa de un porcentaje fijo de las plazas (aunque ese porcentaje depende de la época del año) no es una solución óptima. Si no se producen las cancelaciones esperadas, la imagen del servicio que ofrece la compañía se ve afectada. Dejar pasajeros que han pagado su asiento en tierra siempre tiene repercusiones mediáticas, por mucho que se les compense. Por lo tanto, es necesario encontrar un equilibrio entre los intereses de la compañía, y la percepción de la calidad del servicio por parte de los usuarios.
Aquí es donde la Inteligencia Artificial puede ayudar. Si la compañía pudiera estar razonablemente segura de que una reserva se acabará cancelando, o de que una reserva no se va a cancelar, podría adaptarse de forma adecuada, y minimizar tanto los costes implicados y la pérdida de ingresos, como los efectos negativos en su imagen de marca.
Para este tipo de problemas hay varios modelos de Inteligencia Artificial, englobados dentro del concepto de clasificación, que se pueden testear, para finalmente adoptar el que ofrezca los mejores resultados. El objetivo de la aplicación de estos modelos suele ser doble: por un lado predecir lo mejor posible si una reserva se acabará cancelando y, por otro, determinar los factores (o variables) que más peso tienen a la hora de determinar si una reserva se va cancelar o no.
Cuando una persona efectúa una reserva (ya sea por Internet o presencialmente), se registran una serie de datos. Por ejemplo:
- Fecha de la reserva
- Fecha del vuelo
- Antelación (tiempo entre la reserva y el vuelo)
- Número de pasajeros
- Número de adultos
- Número de niños
- Origen del viaje
- Destino del viaje
- Clase (turista o business)
- Peticiones especiales (equipaje, tipo de comida, mascotas, niños de pecho, traslado desde el aeropuerto, etc…)
- Número de peticiones especiales
- Precio de la reserva
Esta información es lo que en Inteligencia Artificial se conoce como variables independientes (o features). Algunas de estas variables son numéricas (antelación, número de pasajeros, número de niños, número de peticiones especiales, precio de la reserva), otras son categóricas (origen, destino, clase, peticiones especiales…) y, dentro de las categóricas, algunas pueden ser binarias (sí o no, 1 o 0). Para tratar con las variables categóricas, simplemente se codifican también como ceros y unos. Por ejemplo, si una reserva es de clase turista, se le asigna un uno (1), por lo que la clase business será cero (0).
Cada una de las reservas es lo que se denomina observación. Para cada observación, y cuando el dato se registra, se puede añadir una variable más: la etiqueta que dice si la reserva se ha cancelado o no. Es un dato binario, sí o no (1 o 0), y se conoce como la variable dependiente, o variable objetivo, porque es la que queremos predecir.
Cuando se tiene un número suficiente de observaciones, todas etiquetadas de esa forma, es posible “entrenar” un modelo de clasificación que distinga (o separe) las clases de reservas (las canceladas de las no canceladas). En el momento en el que se produce una nueva reserva, el modelo entrenado con los datos recogidos debería ser capaz de clasificarla, y decir si se va a cancelar o no, con cierto grado de acierto. Esto es lo que se denomina entrenamiento supervisado, puesto que se cuenta con la variable respuesta (la etiqueta que dice sí o no, 1 o 0, según se haya producido o no la cancelación), y se pueden comparar las predicciones del modelo con los datos reales. A la hora de entrenar modelos, el objetivo es minimizar los errores o, desde el otro punto de vista, que el porcentaje de aciertos sea el mayor posible.
Términos como Inteligencia Artificial, Machine Learning, y conceptos como el de “entrenar” son armas de doble filo. Por un lado, tienen un efecto mediático innegable. Mueven ríos de tinta, hacen creer a la gente que las máquinas piensan (un efecto potenciado por aplicaciones que ahora mismo están online (que ciertamente ofrecen ejemplos espectaculares), y le dan al tema un aura de ciencia ficción y de gran complejidad. Por otro lado, eso mismo genera reticencias.
El responsable de la gestión de reservas de una compañía aérea no puede confiar en la ciencia ficción y, aunque tenga claro que no lo es, esa sensación de complejidad que alimentan los medios, aunque sea inconscientemente, hace que se plantee seriamente la adopción de soluciones como ésta.
Ni las máquinas piensan (lamento ser un aguafiestas), ni la aplicación de estos modelos es prohibitiva en términos de complejidad técnica y de costes. Lo que hace falta es encontrar a la gente adecuada que sepa del tema y sea capaz de poner el modelo en producción.
Cuando se entrena un modelo de clasificación, y por comentar solo los tipos de acercamientos más comunes, o se busca determinar la influencia de las variables a la hora de clasificar (Regresión Logística), o se busca una forma de separar las clases desde un punto de vista geométrico (Árboles de Decisión, Support Vector Machine, Random Forest, etc…), o se asignan las clases según los vecinos más cercanos (K-Nearest Neighbor).
Hay muchos más, entre los que se cuentan las Redes Neuronales, por ejemplo, pero creemos que explicando los mencionados podremos dar una idea bastante aceptable del concepto.
Regresión Logística
En el primer caso, la regresión logística, el algoritmo de entrenamiento calcula el peso de las variables (el número por el que hay que multiplicar cada variable para otorgarle fuerza en el modelo). Para explicarlo de forma sencilla, sirve este ejemplo: imaginemos que la antelación condiciona mucho si una reserva se va a cancelar o no. A más días de antelación, más probabilidad de cancelar. El algoritmo entonces encontrará un número positivo por el que multiplicar antelación.
Si por el contrario, el número de niños también tiene peso, pero a más niños menos probabilidad de cancelar, el algoritmo encontrará un número negativo para multiplicar el número de niños. Mientras más dependa la variable respuesta de la variable predictora, mayor será el valor absoluto del número por el que se multiplica la variable predictora en cuestión. Si los pesos encontrados por el algoritmo son, por ejemplo 2,6 para antelación y -1,9 para el número de niños, la probabilidad de cancelación dependerá de la siguiente expresión de base:
2,6 * antelación – 1,9 * número de niños
Esta “expresión de base” dibuja una línea que separa las clases:
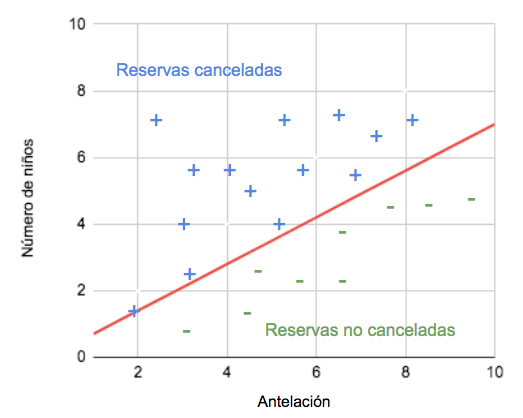
Esta idea se aplica de la misma forma a más de dos variables (pero entonces es más difícil de representar gráficamente). Si una variable no tiene peso, o su peso es muy pequeño (no sirve para determinar si la reserva se va a cancelar o no), el valor absoluto del número por el que se multiplica será cercano a cero.
El algoritmo que busca estos pesos no es mágico, se basa en reglas estadísticas muy conocidas, y muy viejas. Por si alguien está interesado, diremos aquí que los pesos que se dan a las variables son los que maximizan la probabilidad de ver una distribución como la que tienen los datos que han servido para entrenar el modelo (es lo que se conoce como maximum likelihood), y es un tema muy bien documentado.
Solo un apunte más: hemos dicho “expresión de base” porque el cálculo que hemos puesto de ejemplo se utiliza en una ecuación adecuada para calcular probabilidades. Tampoco vamos a entrar en detalles aquí, simplemente basta con decir que la expresión 2,6 * antelación – 1,9 * número de niños se manipula matemáticamente para obtener un valor entre cero y uno. Cero sería la probabilidad nula (la reserva no se va cancelar) y uno la certeza absoluta (la reserva se va a cancelar).
Por defecto, si el resultado de la ecuación es superior a 0,5, el modelo etiqueta a la nueva reserva con un 1. Si es inferior a 0,5, el modelo etiqueta a la nueva reserva con un 0. Es este etiquetado de la nueva observación, la reserva que se acaba de hacer, lo que en la literatura se denomina predicción. El modelo predice que… no es más que la etiqueta que el modelo le ha puesto a la nueva reserva, aplicando la ecuación que se ha encontrado antes.
Intuitivamente, podemos decir que mientras más lejos esté la observación de la línea que separa las clases, más probabilidad (entre cero y uno) tiene de pertenecer a una clase u otra. Si el punto cae justo en la línea, la probabilidad de pertenecer a una clase u otra es del 50%.
Se puede alterar el criterio del 0,5, para potenciar un resultado u otro, pero de eso hablaremos más adelante.
La ventaja de la regresión logística es que como le da un peso a las variables, y ese peso es positivo o negativo según el tipo de relación con la variable dependiente, es muy fácil de explicar, y permite detectar los factores con más influencia.
Es el tipo de modelo que no solo “predice”, si no que además sirve para recomendar cosas del tipo: “si consigues limitar el tiempo de antelación con el que se hacen las reservas, disminuirán en un tanto por ciento las cancelaciones (siempre que el resto de variables se mantengan constantes)”.
Esto suena muy bien, pero la regresión logística tiene sus desventajas. Para empezar presupone que la relación entre variables es lineal, y otras cosas relacionadas con la distribución de los datos. Lamentablemente, el mundo no suele ser lineal, y la distribución de los datos es la que es. Ahora bien, si el modelo arroja resultados aceptables, es muy útil.
Otro enfoque, que exige menos suposiciones sobre la naturaleza de las cosas, es el que podemos llamar como geométrico. En estos casos no se trata de encontrar un peso para cada variable, que permita dibujar la línea que separa las clases, sino de hallar directamente un separador de clases (líneas, planos, o hiperplanos si trabajamos con más de tres dimensiones), basado en la disposición de las observaciones en el espacio.
Árboles de Decisión y Random Forest
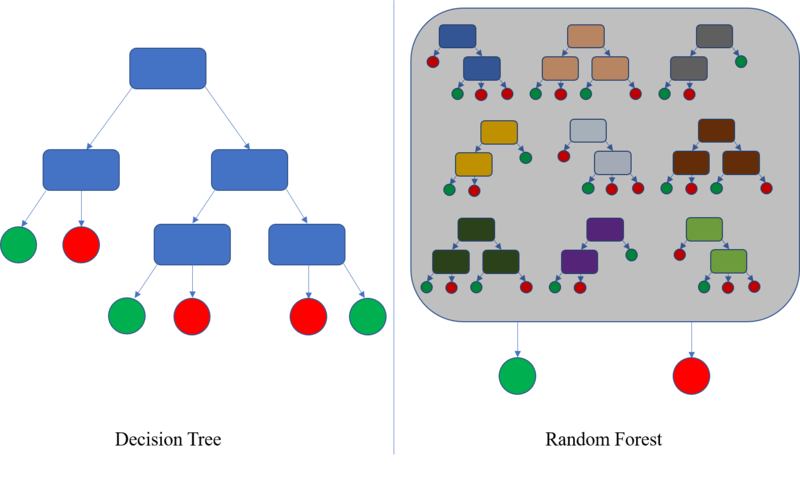
¿Qué es un árbol de decisión? Un árbol de decisión es un algoritmo recursivo, que separa las clases buscando reducir el desorden. En el dibujo superior los rectángulos son nodos, las flechas son condiciones de decisión y los círculos son las hojas del árbol, en las que se reparten las clases sin posibilidad de seguir dividiéndolas (si no se dice lo contrario, todas las observaciones de una hoja pertenecerán a una clase o a la otra).
El nodo raíz, el primero, es la variable que mejor ordena las clases en el sentido de que al separarlas por ese criterio, los grupos resultantes son lo más puros posibles (en uno hay más observaciones de una clase, y en el otro hay más observaciones de la otra).
En el caso de las reservas, supongamos que la clase que mejor divide las observaciones es antelación, y supongamos también que que a partir de 90 días de antelación (unos tres meses), las observaciones se dividen mayoritariamente en entre canceladas y no canceladas. El árbol utilizará entonces antelación como nodo raíz, y trazará una línea perpendicular al eje correspondiente en punto de los 90 días.
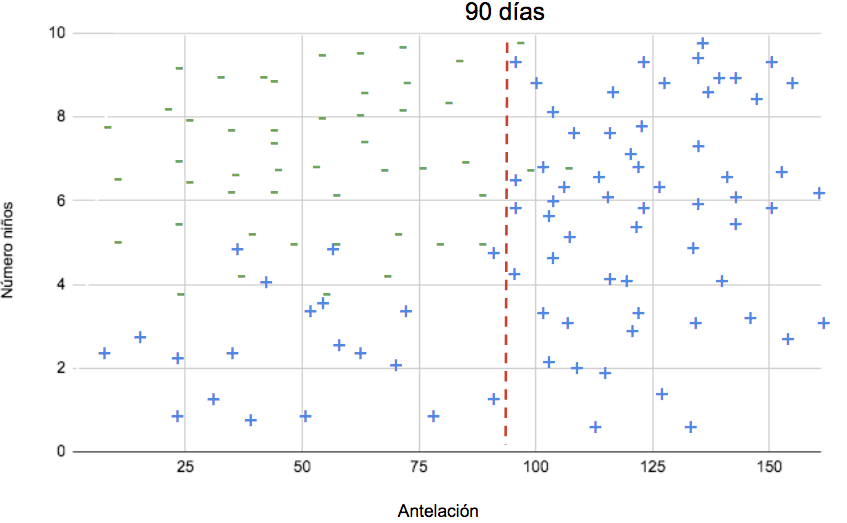
En visualización de árbol, esto sería así:
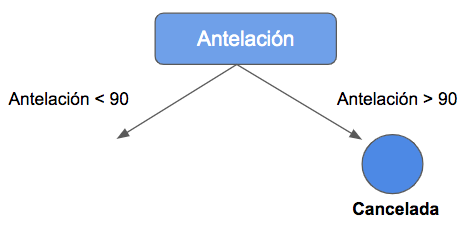
Hacia la derecha, hemos llegado a una hoja. Prácticamente todas las observaciones pertenecen a la clase positiva (reserva cancelada).
Hacia la izquierda aún podemos hacer algo más. Supongamos que la siguiente variable que mejor ordena las clases (recordemos, la que genera divisiones más puras), es el número de niños.
Según el gráfico con la posición de los puntos en el espacio, a partir de 4 niños la mayoría de las reservas pertenecen a la clase 0 (no canceladas). El modelo trazará otra línea, esta vez perpendicular al eje correspondiente al número de niños:
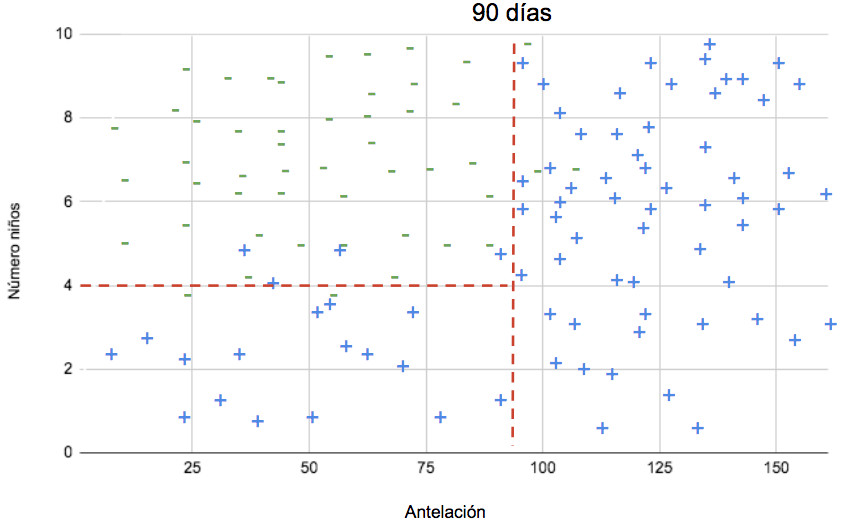
En visualización de árbol, el resultado es el siguiente:
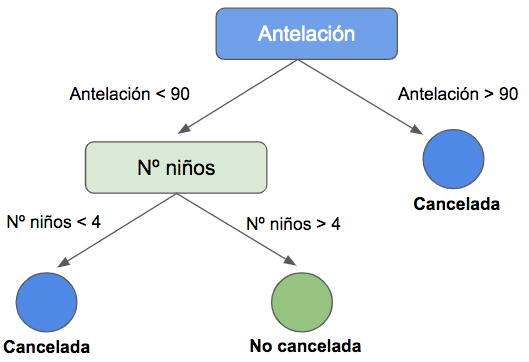
Esto se lee de la siguiente manera: si la antelación es superior a 90 días (hacia la derecha), las reservas se cancelan. Si la antelación es menor a 90 días (hacia la izquierda), entonces la decisión depende del número de niños. Si son menos de 4 (derecha), la reserva se cancela. Si son más de 4 (izquierda), la reserva no se cancela. Evidentemente, se trata de una simplificación para explicar el modelo y su interpretación.
Esto se extiende fácilmente a más variables. El principio es el mismo, y la ventaja del diagrama de árbol es que permite visualizar más de tres dimensiones. Si añadimos variables, van apareciendo nodos.
Según el tipo de árbol que se genere, los colores también significan algo. Si la clase positiva es la azul, y la negativa la verde, un nodo azulado significa que la clase mayoritaria dentro de él es positiva. Si es verde, entonces la clase mayoritaria es la negativa. El tono depende de la proporción. Un nodo con una proporción muy alta de una clase tendrá un tono más oscuro.
La clasificación no tiene porqué ser perfecta. Si nos fijamos en el gráfico de ejemplo, algunas observaciones positivas se quedan al lado de las negativas, y viceversa. Según como se configure el árbol, incluso en las hojas puede haber clases distintas, siempre en proporción mayor una que otra, y la clase se asigna según la que sea mayoritaria.
Todo esto hace de los árboles de decisión modelos muy potentes. No sólo son fáciles de generar, si no que además permiten determinar las variables más importantes, y asignar probabilidades a las etiquetas. La probabilidad de que una reserva se cancele es la proporción de reservas canceladas en la hoja correspondiente.
Si en una hoja tengo 10 observaciones y 8 de ellas se han cancelado y 2 no, la probabilidad de cancelación de una reserva que se asigne a esa hoja será del 80%.
De nuevo, es necesario insistir en que no hay magia detrás de esto… sólo matemáticas. Como se ha dicho, el modelo es recursivo y va seleccionando las variables por orden, empezando por la que mejor separa las clases, y siguiendo por la siguiente que mejor lo hace una vez efectuada la primera división, y así sucesivamente ¿Cómo encuentra las variables? Bueno, diremos que usando algo de teoría de la información y los conceptos de entropía y ganancia de información. Intuitivamente, lo que hace el modelo ya lo hemos dicho: selecciona las variables según su capacidad para ir organizando las cosas. Cada división debe contribuir a separar las clases de la mejor manera posible.
¿Qué es Random Forest?
Random Forest es una ampliación del concepto de árboles de decisión. El principio es exactamente el mismo. La diferencia radica en que en este caso, se cogen muestras aleatorias del conjunto de datos de entrenamiento, y se entrenan varios árboles de decisión seleccionando también aleatoriamente las variables predictoras. Los resultados de cada uno de los árboles generados se ponderan, y la observación se asigna a la clase más votada.
La ventaja de este modelo es que suele tener mejores resultados que un árbol de decisión simple. La desventaja es que perdemos interpretabilidad. Ya no podemos dibujar el árbol (pero sí determinar la importancia de las variables).
Support Vector Machines (SVM)
En este caso el concepto de separación de las clases en el espacio se lleva al límite, por decirlo de alguna manera. Aquí no hay pesos como la regresión logística, ni valores a partir de los cuales se separa una clase, como en los árboles de decisión. Simplemente, se trata de encontrar la línea, el plano o el hiperplano que mejor separa las clases, maximizando el margen que hay entre una clase y otra.
La ventaja de estos modelos es que, si es necesario, son capaces de clasificar las observaciones aun cuando su separación no es lineal o plana. Para ello, usan un truco que supone añadir dimensiones a los datos. Vamos a explicarlo de forma intuitiva, y de nuevo con la ayuda de ejemplos de hasta dos dimensiones, para poder dibujarlo (la base de este ejemplo la he obtenido del material de un curso de Machine Learning del MIT, que recomiendo a todos los que quieran empezar a recorrer este camino).
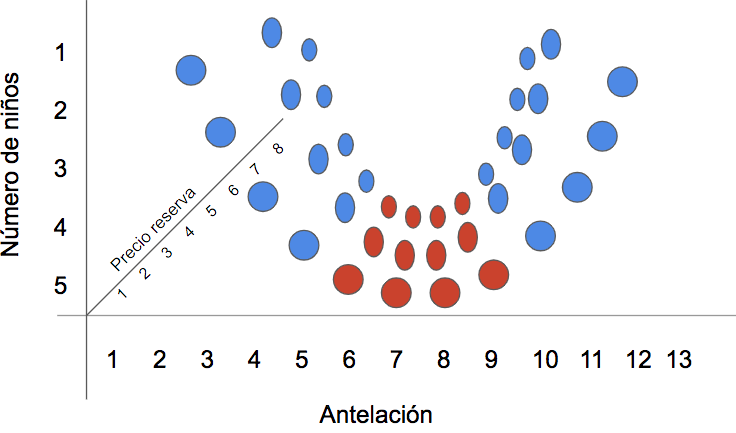
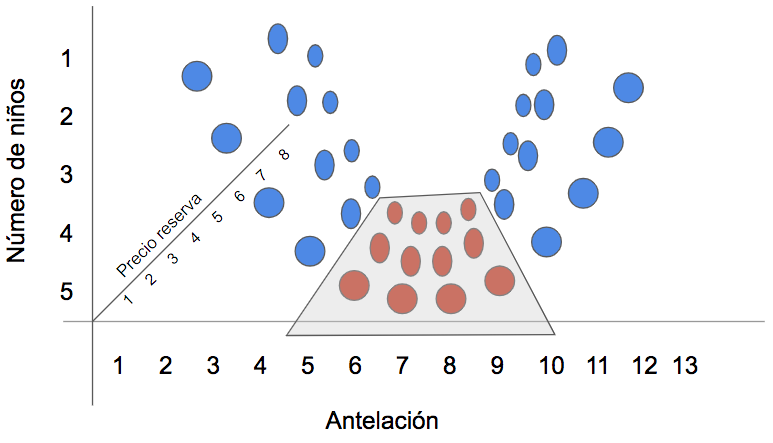
Supongamos que estamos trabajando en una sola dimensión (solo tenemos el dato de antelación). Si los puntos azules pertenecen a una clase, y los rojos a otra, no existe ninguna línea capaz de separar ambas clases:
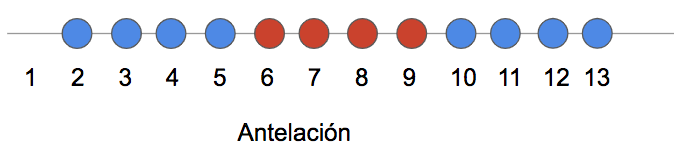
Pero si se añade una dimensión adicional, y se juega un poco con las variables predictoras (por ejemplo, se multiplican por sí mismas), entonces la cosa cambia:
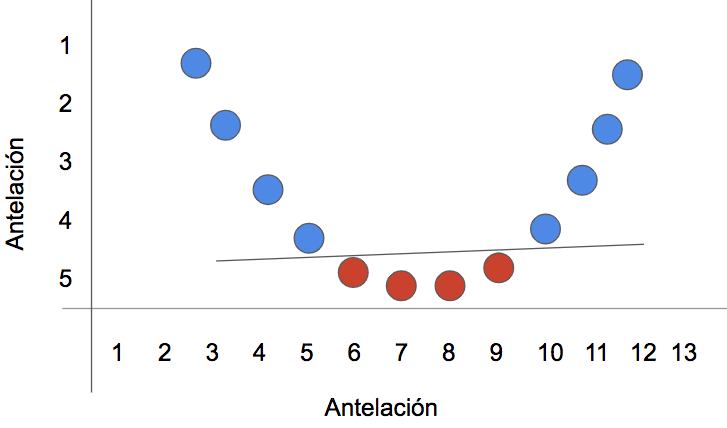
Un inciso sobre support vector machines
Por si no lo hemos aclarado, cuando hablamos de dimensiones simplemente hablamos del número de variables predictoras. El espacio que generan, por ejemplo, antelación y número de niños tiene dos dimensiones (es bidimensional)… Es decir, lo que vemos en el colegio cuando hacemos gráficas cartesianas.
Si añadimos una variable más, por ejemplo, el precio total de la reserva, estamos operando en tres dimensiones (ya es más difícil de graficar).
Si añadimos otra variable, como la clase, entonces estamos en 4 dimensiones y ya no podemos dibujar ejemplos, pero las matemáticas que hay detrás son las mismas.
Cuando se habla de planos e hiperplanos parece que la cosa se complica, pero no es para tanto. Un espacio bidimensional se puede separar con una línea, como en el ejemplo de puntos rojos y azules. Un espacio tridimensional se puede separar con un plano. En el gráfico siguiente los puntos rojos están debajo del plano, y los azules encima. En más dimensiones la idea es la misma, y los planos se llaman hiperplanos.
Aclarado este punto, podemos seguir con la explicación de los modelos basados en SVM.
En este caso, como decíamos, se trata de encontrar la manera de separar las clases lo mejor posible, buscando maximizar el margen entre ellas. En dos dimensiones, la línea que pase entre los puntos, y que tenga mayores márgenes será la que separe las clases. En tres dimensiones, será el plano con mayores márgenes, y en más de tres… pues será el hiperplano que tenga mayores márgenes.
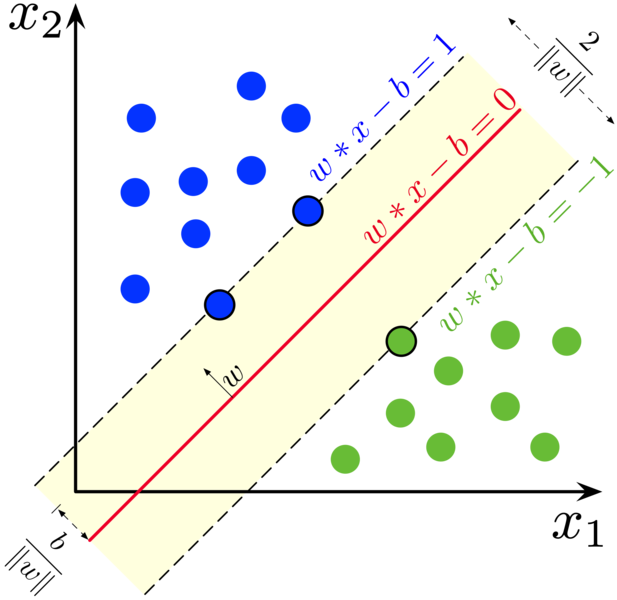
Los puntos que están por encima de la línea se asignan a una clase, y los que están por debajo a otra. Según se quiera ser más estricto o no, se permite o no que los puntos de una clase que caigan en lado “incorrecto” de la línea se sigan asignando a la clase que les toca, si están dentro del margen. El nombre de Support Vector Machine viene de que el modelo busca la línea y sus márgenes tomando como referencia sólo los puntos que están más cercanos entre sí y que pertenecen a clases distintas. En el gráfico anterior, son los tres puntos por los que pasan las líneas punteadas. Esos tres puntos del ejemplo son los vectores importantes. El resto no influyen. Para encontrar esas líneas, el modelo va midiendo la distancia entre los puntos hasta que encuentra la configuración óptima.
A veces, el problema para entender estos modelos es que no se tiene claro qué quiere decir que un punto esté por encima o por debajo de una línea (o de un plano). Vamos a simplificarlo, porque los modelos operan con matrices, y con notación vectorial, pero en el fondo el problema es el mismo, escrito de otra manera.
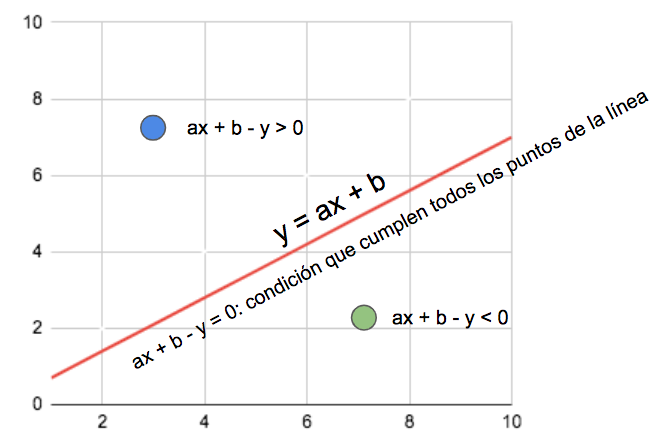
Si tenemos una línea definida por la ecuación y = ax + b, y la reescribimos como
ax + b – y = 0, encontraremos todos los puntos que pertenecen a esa línea. En otras palabras, esa es la condición que cumplen todos los puntos por lo que pasa la línea.
Con esta notación, es fácil ver que si un punto definido por x e y da un resultado mayor que cero, es que está encima de la línea, y si da un resultado menor que cero, es que está por debajo. El mismo concepto se puede extender a planos e hiperplanos.
La desventaja de estos modelos, aun cuando arrojen mejores resultados según qué casos, es que se pierde toda la interpretabilidad. Aquí lo que tenemos es un resultado: esta reserva es de la clase 1, y esta otra es de la clase 0, punto. El modelo no sirve para detectar factores importantes, ni para hacer recomendaciones del tipo “toca esta variable y conseguirás disminuir las cancelaciones”. Si el objetivo es dar un resultado sin más, y que ese resultado sea lo más acertado posible, entonces este tipo de modelos son los adecuados. Pero si queremos entender el mundo, y conocer la relación entre variables, entonces tenemos que confiar en modelos quizá menos exactos, pero más interpretables. A menudo, se usan los dos enfoques… Se entrenan modelos capaces de dar información sobre la importancia de las variables, y modelos que arrojan resultados muy buenos pero que no son transparentes (black boxes).
De nuevo, aquí no hay magia ni pensamiento, solo matemáticas y potencia de cálculo. Lo que hemos estado explicando es posible porque los ordenadores pueden hacer miles de operaciones en segundos. Esto es importante: la teoría que hay detrás de la mayoría de los modelos de Machine Learning es muy antigua. El boom de la Inteligencia Artificial no viene del desarrollo de conceptos matemáticos y estadísticos nuevos, si no la explosión en materia de disponibilidad de datos y capacidad computacional. Incluso las Redes Neuronales, que son lo más avanzado ahora, operan con sistemas similares a los que hemos visto, pero en capas, pasando los resultados de una capa a otra.
K-Nearest Neighbors (KNN)
Para terminar el repaso de los principales modelos de clasificación, veremos brevemente cómo operan los algoritmos basados en la vecindad o la similaridad de las observaciones.
¿Qué es K-Nearest Neighbors? KNN es un modelo que calcula la distancia entre todas observaciones, y asigna las clases según los vecinos más cercanos.
Es importante aclarar que existen otros tipos de modelos, pero con lo visto hasta ahora creemos que ya es suficiente como para tener una idea global, y sirve para demostrar que se pueden adoptar varios enfoques distintos para solucionar la misma clase de problemas. Muy frecuentemente, no sabemos exactamente qué modelo será el que mejor funcione con los datos disponibles, por lo que tener varias alternativas es una ventaja indiscutible.
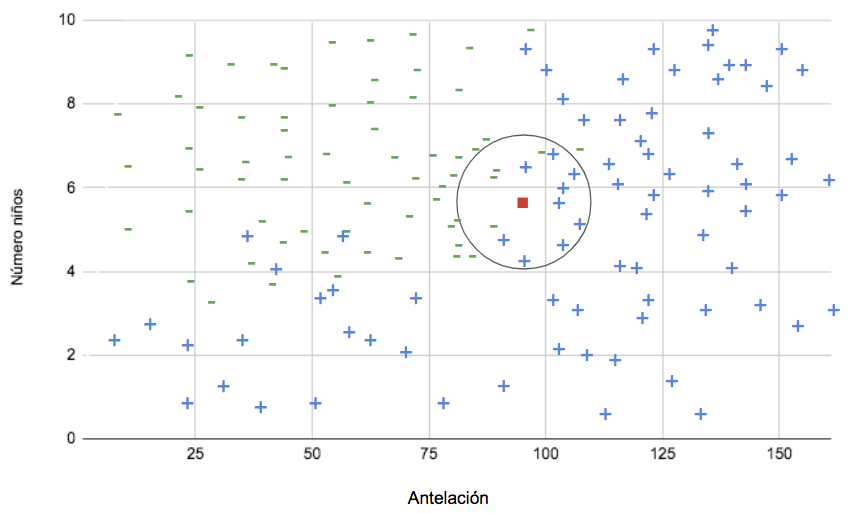
El punto rojo es una observación a la que se le debe asignar una clase. El modelo calcula la distancia entre entre todos los puntos, y según esa distancia y el número de vecinos estipulado (esto es un parámetro que se decide antes de entrenar el modelo), asigna la clase según la mayoría de las observaciones cercanas. En el caso del ejemplo, el punto rojo sería clasificado como positivo.
Si aumentamos el número de de vecinos, la “decisión” del modelo puede cambiar:
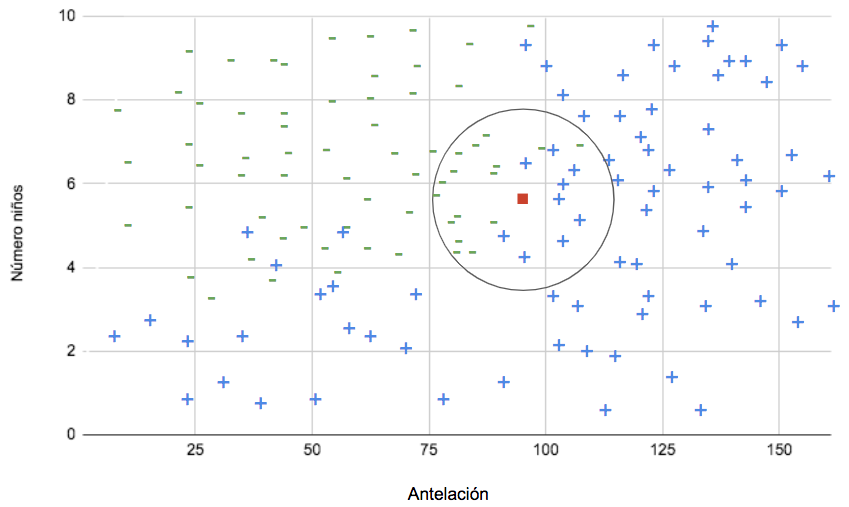
En este caso, hay más vecinos de la clase negativa.
Para calcular la distancia, el modelo puede usar varios criterios, pero el más común es la distancia euclidiana (la que se estudia en el colegio con el nombre de Teorema de Pitágoras).
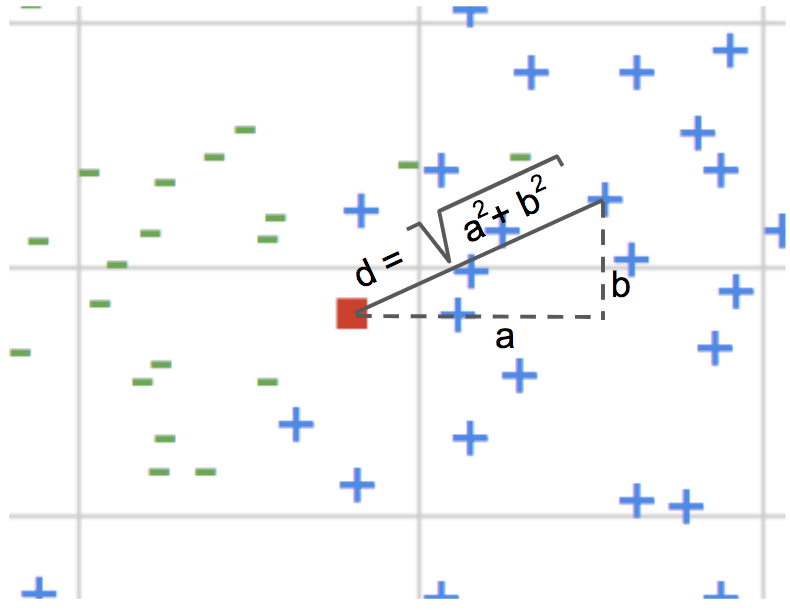
Este modelo es con diferencia el más fácil de entender a nivel conceptual. Las matemáticas implicadas son muy sencillas, y no se basan en reglas estadísticas, ni en teoría de la información, ni en complicadas estimaciones de márgenes aunque, eso sí, tira de máquina porque tiene que calcular la distancia entre todos los pares de puntos.
Criterios de evaluación de modelos
Hemos repasado hasta ahora varios modelos de clasificación, usando como ejemplo la cancelación de reservas. No podemos terminar sin explicar cómo se evalúan los modelos, es decir, cómo se determina si se desempeñan bien o mal con respecto al problema que estamos tratando, y cuál de todos da los mejores resultados.
Para esto, se usa una matriz de confusión. Una matriz de confusión nos muestra los resultados del modelo de la siguiente manera:
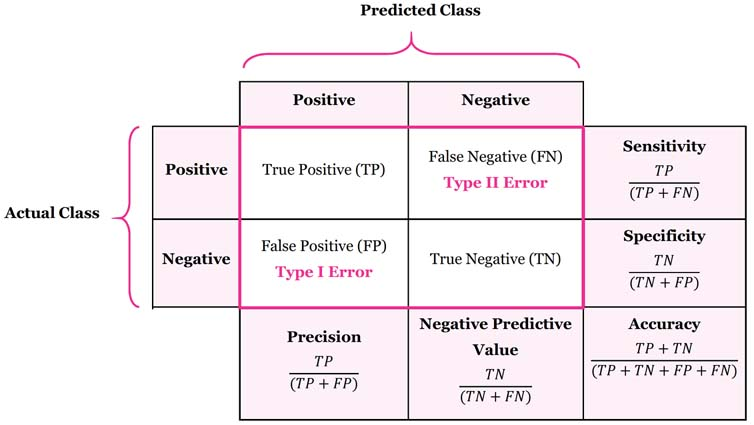
Precisión es el porcentaje de observaciones que se predicen como positivas, y que realmente son positivas.
TP / (TP + FP)
Recall (o Sensitivity) es el porcentaje de observaciones que se predicen como positivas, sobre el total de observaciones positivas.
TP / (TP + FN)
Nota: en Machine Learning, la clase positiva suele ser la de interés. El término “positivo” no tiene un sentido cualitativo. No es bueno ni malo. Es la clase que se marca con 1. Por ejemplo, si nos interesan las cancelaciones de reservas, la clase positiva es la de las reservas canceladas. Si nos interesa detectar tumores malignos, la clase positiva es la de las observaciones etiquetadas como “tumor maligno = 1”. Si queremos predecir si un empleado está contento, la clase positiva son los empleados contentos.
Siempre hay que sacrificar una cosa u otra. Un modelo con alta precisión sacrifica sensibilidad (recall), y un modelo con alta sensibilidad sacrifica precisión.
Dependiendo de la naturaleza del problema, nos puede interesar que el modelo sea preciso (la mayoría de lo que se predice como positivo es realmente positivo, aunque se nos escapen algunos positivos), o que sea sensible (el modelo es capaz de clasificar como positivo la mayoría de los casos que son realmente positivos), aunque eso suponga tener más falsos positivos.
Todo depende del “coste del error”. En los casos en los que un falso positivo tiene menos coste que un falso negativo, entonces tenemos que potenciar la sensibilidad del modelo (recall).
En los casos en los que un falso positivo tiene más coste que un falso negativo, entonces tenemos que potenciar la precisión del modelo.
F1 – score: cuando el coste del error es equivalente, entonces debemos desarrollar un modelo balanceado. En ese caso, la métrica más adecuada es F1 – score (la media armónica entre recall y precisión). Mientras mayor sea el F1 – score, mejor.
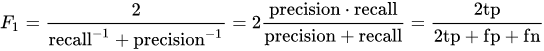
Accuracy: es el porcentaje de observaciones que se han clasificado correctamente.
TP + TN / (TP + TN + FP + FN)
Es una métrica afectada por el balance de las observaciones. Por ejemplo, si la clase positiva es el 10%, un modelo que predice siempre la clase negativa tendría un accuracy del 90%, pero sería un modelo inútil. Accuracy solo es una buena medida del desempeño de un modelo de clasificación cuando las clases tienen tamaños comparables.
Ejemplo de un caso en el que el modelo debe ser sensible
Un modelo para determinar si un paciente tiene cáncer o no (siendo “tener cáncer” la clase positiva) debe ser muy sensible (recall), puesto que el coste de un falso positivo es mucho menor que el de un falso negativo. Si el modelo dice “tiene cáncer” cuando en realidad la persona no lo tiene (falso positivo), se aplicará el protocolo y se iniciará un tratamiento. El coste es un susto, y quizá algo de dinero para la Seguridad Social, hasta que se determine que en realidad no hay cáncer.
Pero si el modelo predice “no tiene cáncer” cuando la persona realmente tiene cáncer (falso negativo), el coste del error puede ser la vida de la persona.
Ejemplo de un caso en el que el modelo debe ser preciso
Un modelo para predecir si un fondo de inversión es bueno o no, debería ser muy preciso. Es decir, el porcentaje de lo que se predice como bueno (clase positiva), y es realmente bueno, debe ser muy alto. De lo contrario, podríamos invertir el dinero en un fondo malo y perderlo. En este caso, el coste de decir “este fondo es bueno”, cuando en realidad es malo (falso positivo), es mucho mayor que el de un falso negativo (este fondo es malo, aunque en realidad sea bueno). Nos estamos perdiendo algún fondo bueno, es verdad, pero disminuimos el riesgo de perder dinero (este ejemplo también proviene del material del curso del MIT mencionado anteriormente).
Ejemplo de un caso en el que el modelo debe balancear precisión y sensibilidad
Este caso de estudio en concreto puede ser ejemplo de un modelo balanceado. Si el modelo genera muchos falsos positivos el hotel revenderá habitaciones reservadas que al final no se cancelan, perjudicando al cliente, y la percepción de la calidad del servicio entre los usuarios. Si por el contrario genera muchos falsos negativos, el hotel sufrirá una merma en sus ingresos al no tomar medidas para disminuir las consecuencias de una cancelación. Para los modelos que deben balancear sensibilidad y precisión, la métrica adecuada es F1 – score.
Con esto hemos repasado los principales conceptos relacionados con los modelos de clasificación, y cómo pueden ayudar a gestionar el problema de la cancelación de reservas. Es importante destacar que ésta es sólo una de sus posibles aplicaciones. Tal y como se ha puesto de manifiesto en los ejemplos anteriores, estos modelos se pueden utilizar en medicina, marketing, decisiones de negocio e inversión, etc.
